How damage rolls work and why multi-hit moves deal more consistent damage

Damage rolls are probably one of the most frustrating parts of playing competitive Pokémon. Getting a bad rolls can mean that you don’t get the KO on an opposing Pokémon, leaving it free to attack one more time, which could be all your opponent needs to win the game. There is however a way to reduce the variance in you damage rolls. Ironically, it requires your Pokémon to attack multiple times.

How does Damage Calculation work?

How much damage an attack deals is calculated via a formula that is dependent on multiple variables:

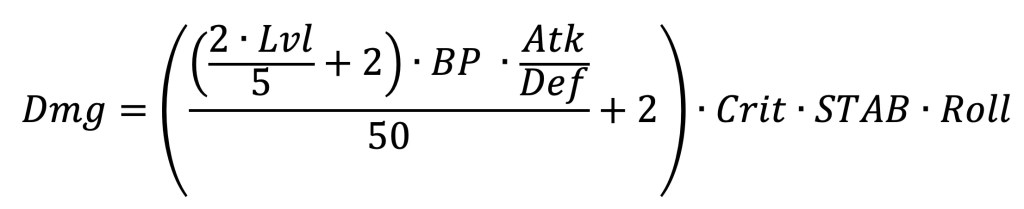
Dmg: Damage dealt

Lvl: The attacking Pokémon’s level (always 50 in VGC)

BP: Base power of the attack

Atk: The attacking Pokémon’s attack or special attack stat 

Def: The defending Pokémon’s defense or special defense stat

Crit: 1.5 if critical hit, otherwise 1

STAB: Same type attack bonus, 1.5 if move type matches the attacking Pokémon’s type, otherwise 1

Roll: Any integer from 85 to 100, then divided by 100 (0.85 ≤ Roll ≤ 1)

There are a few more multipliers that can apply, such as effectiveness of the move, weather, or items such as Choice Band, but let’s leave them aside to keep thing as simple as possible.

This means that there are 16 possible damage rolls for an attack: one for every integer from 85 to 100. All these rolls have the same chance of occurring, 1 in 16 or 6.25%. However, there is still one problem: HP can only be calculated in rounded integers, not in decimal numbers. This is where the damage calculation starts to get a little strange: Not every operation is rounded equally.

Rounding

Some operations are rounded regularly to the nearest integer with the exception that .50 is rounded down instead of up.

Others however are always rounded down to the nearest integer, or floored. This can be shown in the equation by using different kinds of brackets: curly for rounding, and square with the top missing for flooring, so called floor brackets.

The following table shows which multipliers are rounded and which are floored:

Wicked Blow: Single Hit

252+ Atk Urshifu-Single Strike Wicked Blow vs. 252 Def Snorlax on a critical hit: 109-130

We have an Urshifu Single Strike using its signature move Wicked Blow against a Snorlax with 252 Defense EVs, which will act as out punching bag. From the calculation we get the following damage rolls:

(109, 111, 112, 114, 115, 117, 118, 120, 120, 121, 123, 124, 126, 127, 129, 130)

We can plot these in a graph to show the probability of each damage roll. This kind of graph is called a histogram.

We can see that the distribution is mostly flat, except for 120, which can occur twice because of rounding. There is a 1/16 chance of landing the highest roll and dealing 130 damage, but there is also a 1/16 chance of landing the lowest roll, 109.

Let’s say you need to get a roll in the upper two thirds of damage dealt to get the KO, in this case that would be 117 damage or more. If you need to deal 117 damage to your opponent’s Pokémon, you don’t care about the 10 rolls that result in more than 117 damage being dealt, that’s all fine. What you do care about is the 5 rolls that result in less damage, because that 5 in 16 chance of not taking the KO could cost you the game.

However, this kind of flat distribution only applies to single-hit moves. There is a way to reduce the variance in how much damage you deal, thereby reducing the likelihood of an especially low roll occurring: Landing multiple hits.

Surging Strikes: 3 Hits

Urshifu Rapid Strike’s signature move Surging Strikes is essentially the same move as Wicked Blow. It has a total Base Power of 75, is boosted by the Same Type Attack Bonus, and always lands a Critical Hit. The only difference is that it lands three hits with a Base Power of 25 each, instead of one hit with a Base Power of 75.

252+ Atk Urshifu-Rapid Strike Surging Strikes (3 hits) vs. 252 Def Snorlax on a critical hit: 111-135

We can see that the rounding errors actually cause Surging Strikes to do more damage than Wicked Blow, despite them having the same Base Power. These are the rolls for each hit:

(37, 37, 39, 39, 39, 40, 40, 40, 40, 42, 42, 42, 43, 43, 43, 45)

The final damage rolls are the sums of every possible combination of rolls for the individual hits.

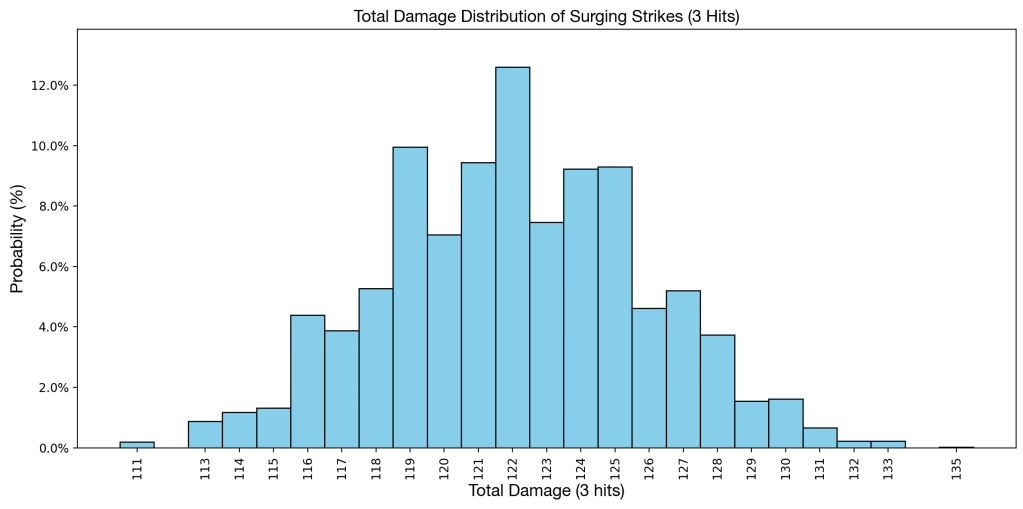
We can see that the distribution of how much Damage Surging Strikes is going to deal looks more like a bell curve, different from the mostly even distribution of Wicked Blow. This makes a high roll extremely unlikely.

In this example there is only one combination of rolls that results in dealing 135 Damage. Each hit would need to land the maximum Damage Roll of 45. Since each hit has a chance of 1/16 of being 45, the probability of dealing 135 damage is 1/(16x16x16) or 1/4096, which equates to 0.024%.

However, this also means that Surging Strikes is an incredibly consistent move! A high roll may be unlikely, but so is a low roll, meaning that you can usually rely on a move taking a KO if you specifically calced for it.

Let’s again assume that we need to get a roll in the upper two thirds of damage dealt to get a KO, in this case that would be 120 damage or more. With this distribution of probabilities, Surging Strikes would have a 72.9% chance of taking the KO, since 2987 out of a total 4096 possible combinations of damage rolls would result in a KO. For comparison, Wicked Blow should only have a two thirds or 66.67% chance of landing a damage roll in the upper two thirds, although in reality it’s 68.75% due to rounding errors. This deviation only gets more extreme the closer you get to the edges of the bell curve.

Conclusion

While it may seem counterintuitive, Surging Strikes is actually more consistent than Wicked Blow. Since the multiple Damage Rolls tend to cancel each other out, you are very unlikely to land a high or low roll and will instead most of the time stay in the middle. In contrast, Wicked Blow has an even distribution among the probability of its damage rolls, meaning that a high roll is just as likely as a low roll or a medium roll. 

I hope you enjoyed my new article! Please let me know if you’d like to know more about how damage calculation works for multi-hit moves. Maybe I’ll torture myself by calculating all possible rolls for Scale Shot and Population Bomb.